Neurocomputation – Elaine Reynolds

Some time ago I began collaborations with two of my colleagues in Computer Science at the intersection of our fields, neurocomputation.

A Netlogo Model of the N signaling pathway

The Notch (N) signaling pathway is involved in cell fate decision and developmental patterning in diverse organisms. We have developed an Agent-Based model of this pathway as characterized in the early Drosophila embryo that represents the major molecular components of the pathway and allows us to control the levels of these components, their transition from one state to another and their movement from the nucleus to the cell membrane and back. Most steps introduce randomness into the system using probabilities of events. We are using the model to investigate how specific molecular components that act to stabilize fate at the cellular level also are involved the formation of pattern in the larger group of cells.

A data logging mechanism captures an integer count of cells with a neuronal fate (as defined as a lack of N product) and cell levels of N at each time step and stores them to a text file as a number sequence that preserves cell position, linking cell behavior to pattern dynamics. Parameters that produce a stable pattern exhibit oscillations before setting into a stable pattern. Using a plot of neuron count vs. time of either single run or aggregate data, we can assess a stabilization time using a measure of deviation, the final count of neurons, and an assessment of pattern that can be compared to an optimal pattern. To quantitate pattern, we use a modification of Hamming distance that measures the amount of dis-similarity at successive spatial positions within the model.

Within a wide set of initial parameters, our current model can accurately reproduce the rosette pattern of neurons and skin cells. We have explored the roles of initial transcriptional rates, the endocytic processing of Dl, transport and processing of N after cleavage, and the regulation of transcription by N. Results indicate that initial transcription rate can be varied and a stable pattern is still obtained. There is a sweet spot where stabilization rates are long enough to allow a proper pattern to form, similar to the ideas of landscape first proposed by Waddington (1959). Dl and N processing parameters shift the optimums in this landscape, but overall do not disrupt the formation of pattern. However, the model only achieves the proper pattern and number of neurons when there is transcriptional feedback to N and Dl expression.

Related abstracts and publications:

Himmelwright R*, Pfaffmann JO, Reynolds ER (2013) A NetLogo model of the Notch regulatory network in the determination of developmental patterning. Program No. 588.06, 2013 Neuroscience Meeting Planner, San Diego, CA: Society for Neuroscience. Online

Reynolds ER, Himmelwright R*, Sanginiti C*, and Pfaffman J (2015) From cells to pattern: A NetLogo model of the Notch signaling. A. Conf. Dros. Res. 55: 776A

Pfaffmann JO, Reynolds ER, and Ruebeck C (2013). Competitive behavior in a loosely-coupled biological cell network game. Western Economics Association International (WEAI) 88th Annual Conference, Seattle, Washington. Conference paper

Reynolds ER, Himmelwright R*, Sanginiti C*, and Pfaffman JO (2019). A NetLogo model of the Notch regulatory network in the determination of developmental patterning. BMC Syst Biol (2019) 13: 7. https://doi.org/10.1186/s12918-018-0672-9

System Difference: A new measure based on degree linking information theory and network graph analysis

We started this project with a group of neuroscience majors who had taken my Intro to Neuroscience class and were interested doing research on consciousness. At the time, one research group had created a formal theoretical definition for consciousness. Giulio Tononi and collaborators proposed that consciousness was “the capacity to integrate information” and that neural systems with a large capacity would be conscious. To measure this property, they developed a way of calculating Effective Information (EI), a measure of all the causal interactions between two subsets of nodes in a system. Their new variable, Phi (Φ) is a measure of the EI that can be shared across the subsets of a system (3). Like others, they felt that neural system that could integrate information would have two basic properties: specialization, a high degree of node structure variance; and connectedness, the ability to reach any node from any other node. Phi as a measure captured these properties as well. However, Phi was complicated and computational expensive and so it remained theoretical. Several revisions and updates of the original Phi have improved the measure.

We built on their work by trying to capture characteristics of high Φ matrices into our own variables. We calculated Φ and our variable measures over a large, random sample of connection matrices. Then we analyzed how well our variables explained Φ. One particular variable, SD or system difference, correlated well with Φ in various measures.

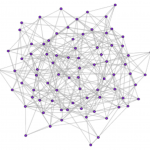Exploring the role of hub structures in the changing properties of functional networks

The structural and functional connectivity of the brain forms complex networks that can be characterized using classic graph theory and informational analysis. While our understanding of that connectivity is incomplete, previous research has suggested that these networks display small-world (sw) properties, a pattern of connections that optimizes information flow (Watts & Strogatz, 1998, Sporns & Honey, 2006). These sw properties of functional networks and the flow of information appear to break down during unconscious states (Uehara et al., 2013, Ferrarelli et at., 2010). To explore the breakdown of these networks, toy sw graphs were altered by several algorithms: a random algorithm that selects and moves edges in the network randomly, and several hub algorithms that move edges by first attacking the edges between hubs, and then the edges between hub and non-hub nodes. Each hub algorithm used a different method to define hub nodes: Eigenvector Centrality, Betweenness Centrality, and node degree. The results suggest that hubs as defined by different algorithms produced altered graphs that were different in terms of their role in global network properties. The hub definitions used do not always define hubs that are involved in maintaining or breaking down sw properties. As research on functional brain networks moves forward, locating and defining the different types of hubs within a network will help provide insight into the role each region may play, as well as how much control that region can influence on the global functional network.

Related abstracts:

Himmelwright R* and Reynolds ER (2014) Exploring the role of hub structures in the changing properties of functional networks. Program No. 760.01, 2014 Neuroscience Meeting Planner, Washington DC: Society for Neuroscience. Online