IDA Implementation by R. E. Andersen ’06 and J. P. Rowe ’06
Our algorithm is designed to efficiently compute the probability that a Boolean function will be true. It does this by performing an independent-disjoint analysis (IDA) of the function, rewriting the function recursively using sums and products of simple formulas that are pairwise independent or disjoint. (A “simple formula” is one in which no variable appears more than once.) We can then recursively assess the probability that the function is true using these facts: independent events have P(AB)=P(A)P(B) and P(A+B)=P(A)+P(B)-P(A)P(B), while disjoint events have P(AB)=0 and P(A+B)=P(A)+P(B). The time required for this recursive assessment is linear in the number of simple formulas that appear in the IDA. For this reason we call such a rewritten form of the function “easily countable.” Our program analyzes a Boolean function using the IDA algorithm, then outputs an easily countable form of the function, along with the probability that the function will be true (presuming the variables are true independently with probability .5). After downloading Ida.jar and IDA.bat, input and output can be done through the keyboard/interactions window, or through files.
Note: When presented with a large example, the program may return an error message indicating that it should be run again. The program will automatically reset a default parameter at a higher value for the next attempt.
Instructions for downloading IDA
1. Download and run JRE 5.0 update 4 or later (the third link down) at
http://java.sun.com/j2se/1.5.0/download.jsp
It may also be necessary to install netBeans.
2. Create a folder IDA on your hard drive.
3. Right-click IDA.bat, select Open and then Save the file to the IDA folder. (If opening the file does not prompt you to save the file, right-click IDA.bat, select Save Link As or Save Target As, and save the file in the IDA folder.)
4. Right-click Ida.jar, select Open and then Save the file to the IDA folder. Make sure to change the name to Ida.jar if it is given as Ida.zip, and/or change the file type to “all files” instead of “zip files”.
5. Double click on IDA.bat to start the program.
Instructions for running IDA
If you choose to use files for input and output, please put the input file in the following format.
list of variables, with a space between each and the next
boolean function (minpaths separated by plus signs)
Here is a simple example.
a b c d e f g h
ab + cd + ef + edh + begh + adg + afgh
The output will look like this.
Original function: ab + cd + ef + edh + begh + adg + afgh
Easily countable function: d((h+f)e+c+(b+g)a) + ~db(e(f+hg)+a) + (ahg+e)~d~bf
number of easily countable disjoint terms: 3
Probability this function will be true: 163/256
In the output, a ~ negates the variable or expression in parentheses that follows it, and terms which are to be multiplied (conjuncts) are written next to each other. For instance (ahg+e)~d~bf represents ((a&h&g) or e)&(not d)&(not b)&f.
Here is the program’s analysis of a famous example, due to J. A. Abraham [IEEE Trans. Reliability R-28 (1979), 58-61].
Input:
a b c d e f g h i j k l
jkl + bcjl + acdh + dfhk + acfjl + bcdfh + abdhk + ghijk + efghk + acegh + efikl + aceil + dehijk + abeghk + bcefgh + bcghij + abeikl + bcefil + dfgikl + acdgil + acfghij + bcdehij + bcdfgil + abdgikl
Output:
Easily countable function: ((e+f+a)d+l+g)ijhc(k+b) + ~ijhc(k+b)(l+(d+eg)(f+a)) + ((il+g)e+d)~jhc(k+b)(f+a) + (d+l+(i+e)g)~(k+b)hcajf + ~(k+b)hca~(jf)((il+g)e+d) + (f+ab)kh~cj(d+l+(i+e)g) + (e(g+il)+d)(f+ab)kh~c~j + (i(de+g)+l)j~(f+ab)kh~c + ((a+b)c+k)(j+f)~hli(dg+e) + (kb+c)a~hli(dg+e)~(j+f) + ~(i(dg+e))j~hl((fa+b)c+k)
number of easily countable disjoint terms: 11
Probability this function will be true: 1309/4096
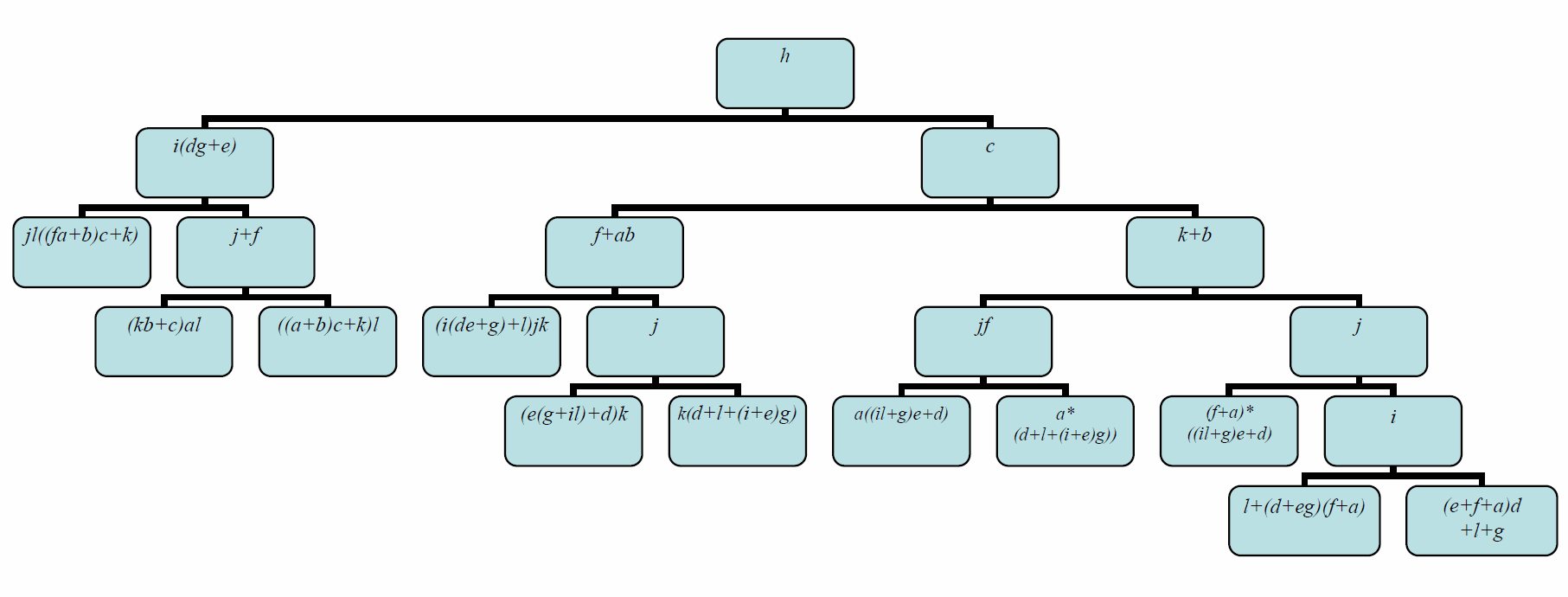
Here is a different view of the program’s IDA analysis of Abraham’s example, as a binary decision diagram with variable transformations at the nodes. Each node represents an expression, and under each node the left-hand link represents the negation of that expression and the right-hand link represents the assertion of that expression. (Technically, there should be left-hand links to 0 and right-hand links to 1 from the nodes at the bottom of the diagram; these links have been omitted for simplicity.)
The 11 nodes at the bottom of the diagram represent the 11 terms of the IDA analysis. For instance the left-most bottom node is reached by using the left-hand links under the nodes marked h and i(dg+e); this node represents the last term of the IDA analysis, in which h and i(dg+e) are negated and the expression represented by the node, jl((fa+b)c+k), is asserted.
If the graphic below is difficult to see, you can click on it for a larger version or click here for a pdf version of this page.