Research Interests
I am a Lie theorist by training, and have interests in Lie groups, Lie algebras, and representation theory. My dissertation extended two results on converging matrix sequences to a more general Lie groups context; in particular, I showed that the iterated Aluthge sequence and the Bruhat sequence converge under a few restrictions in any real noncompact semsisimple Lie group.
I am currently studying another problem involving the generalization of matrix-theory results to Lie groups, as well as multiple derivations on semisimple Lie algebras. In the future, time permitting, I plan to study honeycombs, as well as asymptotic representation theory.
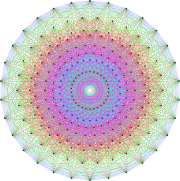
The graphic on the left, courtesy of Wikipedia, is a 2 dimensional projection of the root system of a 248 dimensional Lie group known as E8. The graphic beautifully illustrates the incredible symmetries of the group.
An incredible body of information about Lie groups and Lie algebras has been compiled by the Atlas of Lie Groups Project.
CV
Publications
- The Convergence of the Bruhat Iteration, submitted for publication.
- Convergence of Aluthge Iteration in Semisimple Lie Groups, to appear, Journal of the Mathematical Society of Japan.
- Determinants of Sums of Two Real Matrices and Their Extensions, Linear and Multilinear Algebra 60 (2012), Ky Fan Special Issue, 1409-1431.
- Determinant of Sum of Orbits Under Compact Lie Groups, Linear Algebra and its Applications 436 (2012), 1644-1650.
- Determinant and Pfaffian of Sum of Skew Symmetric Matrices, Linear Algebra and its Applications 433 (2010), 412-423.