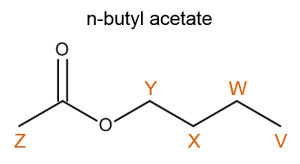
The following spectrum corresponds to a mixture of ethyl bromoacetate and n-butyl acetate in CDCl3 with TMS as a standard.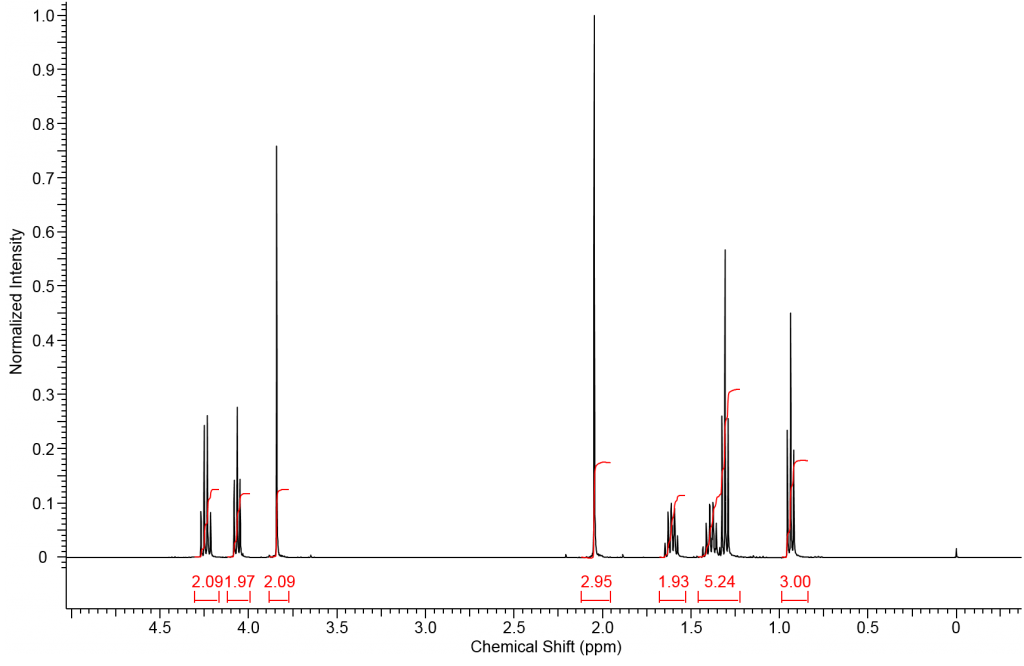 
You were told that the mixture is a perfect 50:50 mixture of the two substances and asked to confirm this by NMR. Assuming the mixture is not volatile you could determine the relative amount of each substance using integration.
First we draw each molecule and label the equivalent protons. It is best to analyze each molecule and determine what resonance features we would expect to see in the spectrum.
 |
Ethyl bromoacetate has three sets of equivalent protons that should appear in the following manner.
|
||||||||||||||||||||||||
 |
The 5 resonance peaks for n-butyl acetate would be expected to show up in the following pattern.
|
The simplest way to identify each compound within the spectrum is to determine a peak from each compound that we can identify easily. The two singlets will be the easiest to identify. Which singlet corresponds to protons A and which to protons Z?
 |
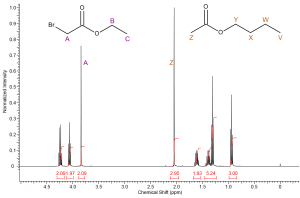If we consider what we know about deshielding and chemical shift it should be clear that methylene A will resonant downfield of methyl protons Z; therefore we can identify the singlet at 3.8ppm as corresponding to methylene protons A and the singlet at 2.05ppm clearly corresponds to methyl group Z. |
 |
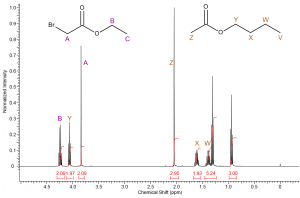We can now label most of the remaining resonance peaks without much issue. Methylene B must correspond to the downfield quartet (4.25ppm) resonance just as methylene Y must correspond to the triplet at 4.05ppm. The quintet at 1.60ppm and the sextet at 1.38ppm are easily identified as protons X and W respectively. |
 |
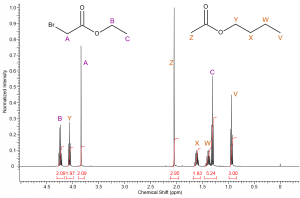Methyl protons C and V must correspond to the two remaining triplets. Again using your knowledge of deshielding you should be able to determine that the resonance corresponding to methyl group V should be the farthest upfield (most shielded). Therefore, the triplet at 1.31ppm must correspond to methyl group C and the triplet at 0.94ppm represents methyl group V. |
In reality only one peak from each compound needs to be identified; however, best practice is to ensure all the peaks have been correlated to the appropriate compound in order to avoid misidentification.
To determine the relative concentration of each compound in solution we must realize that each integration value corresponds to the number of that proton type in solution. If we had an internal standard for which we knew the exact concentration we could use it to determine the exact concentration of each compound. However, for this spectrum we only know relative concentrations. If the mixture was exactly 50:50 then the integration ratio of B:Y would be 1:1 as both peaks represent 2 protons in their respective compounds. The following table shows other ratios we might expect.
| Ratio of C4H7BrO2 : C6H12O2 | Peaks Compared | Ratio of Integral values |
| 1:1 | B:Y | 1:1 |
| 1:2 | B:Y | 1:2 |
| 4:1 | B:Y | 4:1 |
| 1:1 | A:Z | 2:3 |
| 1:2 | A:Z | 2:6 or 1:3 |
If we compare two peaks representing the same number of protons in each compound (B:Y) we should expect the ratio of integral values to be the same as the ratio of compound concentration. However, when resonance A is compared to resonance Z the integral ratio will be different than the ratio of compounds because resonance A corresponds to 2 protons and resonance Z corresponds to 3 protons. In a solution containing a 1:1 mixture of the above acetates the relative concentration of Z would be 1.5 (or 3/2) times that of the concentration of A.
 |
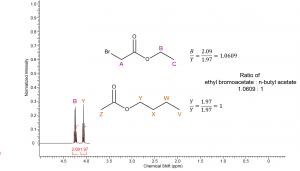How do we determine the relative ratio of compounds if we know the relative integration values? If we can compare two integrals that represent the same number of protons in each compounds, such as peak B and Y then we simply divide each number by the lowest integral value to determine the ratio of ethyl bromoacetate : n-butyl acetate. |
 |
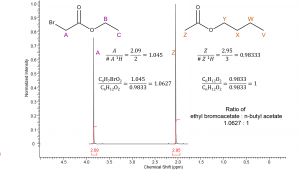Any two integral values, assuming they represent different compounds, can be compared to determine the relative amount of each compound. Comparing compound A and Z requires the integral values to be divided by the number of protons represented by each resonance. This converts the integrals to the # of molecules rather than # of protons. Notice this procedure gives the same relative ratio of ethyl bromoacetate : n-butyl acetate. |
The mixture is not an exact 1:1 mixture of bromoacetate : n-butyl acetate; however, it is very close at 1.06:1.