Specifications Report
Table of Contents
General Specifications and Functional Requirements
Introduction
In any engineering endeavor, it is critical to define the design parameters that will ultimately guide development decisions on the course to the final product. These parameters, or specifications, often can be derived from our functional requirements and are characterized by establishing whether the goal of the specification is to minimize, maximize, or target a specific value. Based on the goal, lower and upper bounds are set in addition to a constrained value, if applicable. Recognize that a constrained value describes the absolute minimum or maximum the system must meet in order to satisfy the specification’s requirements. In this report, each sub-team has outlined several specifications they have determined necessary in developing their respective sub-systems. The teams have provided a table of all of their identified specifications followed by supplementary descriptions to provide additional clarity as to each specification’s purpose and meaning. We have also included general specifications for the overall robot in this report.
General Specifications and Functional Requirements
| # | Type | Name | Min, Max, or Target | Lower Bound | Upper Bound | Constrained Value (if applicable) | Units |
| G1 | Specification | Carrying Capacity | Maximize | +10 | ∞ | Weight of robot components | kg |
| G2 | Functional Requirement | Weight of Robot | Minimize | 0 | 40 | 50 | kg |
| G3 | Functional Requirement | Power Consumption | Minimize | 0 | 1000 | 1500 | Watts |
| G4 | Functional Requirement | Cost | Minimize | 0 | 3000 | 4000 | USD |
| G5 | Specification | Durability | Maximize | 50 | ∞ | 10 | cm |
- The “Carrying Capacity” specification is the total additional weight the robot can effectively carry while continuing to satisfy other specifications, including those for minimum land speed, power consumption, and more. This specification could be split into sublevels that delineate the effective carrying capacity on land, in water, or in other scenarios. The goal is to maximize the carrying capacity of the robot to demonstrate that it could prove itself as an effective disaster relief solution in providing essential resources to victims. Ideally, we believe the robot should be able to support an additional 6 kgs (enough for 3 liters of water, 2 first aid kits, and some food); however, the robot, at a minimum, must be able to support its own weight. With this additional weight, we could add a first aid kit in addition to food and water.
- The “Weight of Robot” specification is the maximum functional weight for the fully integrated robot. This specification is dependent on the interfaces of all the four major subsystems. The goal is to minimize weight, as the application would ideally allow for multiple HARRT robots to be dispatched in emergency situations. Any extraneous weight could hinder its ability to deliver aid and limit maneuverability in the desired terrains, and impact the extent of human interaction with the robot. To achieve this goal, the material choice and allocation have been designed to reduce the total weight.
- The “Power consumption” specification is the peak wattage the robot should draw while operating. This specification does not include the land and water movement chassis together, but rather each individually. If a joint chassis is constructed, it will be subjected to the 1500 W max constraint, however. The driving factor behind the choice of 1500 W maximum recommended is the power output capacity of a standard 15 Amp, 120 Volt wall outlet, which will likely be plenty powerful enough for the HARRT robot’s application.
- The “Cost” specification is the cost of the entire design, development, and manufacture of the HARRT robot. This includes the material and manufacturing costs associated with the construction of all prototypes made during the design process, as well as those involved in the construction of the final product. While there is no explicitly stated upper bound on the team’s budget, other than an indefinite reference to the “low thousands of dollars,” it seems reasonable to assign the upper bound of $3000 and a constraint of $4000. Satisfying this specification requires consideration during all stages and areas of design. Most often, this is manifested by efforts to minimize the reliance upon purchased components and simplify manufacturing processes whenever possible. Generally, efforts to improve performance in other specification areas are in conflict with the goal of minimizing costs as components that are stronger, lighter, more efficient, etc. are also usually more expensive.
- The “Durability” specification is the maximum height from which the robot can drop without sustaining serious damage. It is reasonable to expect that the robot could tip over while its legs are in the fully extended position, meaning the body of the robot will be about 50 cm above the ground, thus motivating our choice for the lower bound on this specification. Meeting this specification requires that structural components like the legs and chassis be designed with factors of safety to ensure the robot’s continued functioning in the event of impact loading. Additionally, delicate components like electronics will need to be shielded from direct impact and possibly protected from shock due to remote impact.
Swim Specifications
| # | Type | Name | Min, Max, or Target | Lower Bound | Upper Bound | Constrained Value (if applicable) | Units |
| S1 | Functional Requirement | Thrust Force | Target | 170 | 180 | N/A | Newtons |
| S2 | Specification | Forward Velocity | Target | 5 | ∞ | N/A | MPH |
| S3 | Functional Requirement | Power Consumption | Minimize | 0 | 150 | N/A | Watts |
- The “Thrust Force” functional requirement is the force on the robot as a result of the Centrifugal Pump “pumping”. To begin estimating the robot’s thrust force, the robot was modeled as a 20 x 20 x 20-cm square prism, with a \(C_d\) and \(\rho\) of 2.2 and 998 \(kg/m^3\), respectively. Upon further iteration, however, the model was reduced to a 20 x 20 x 20-cm square prism, having a \(C_d\) and \(\rho\) of 2.2 and 998 \(kg/m^3\), respectively. Additionally, the robot’s desired maximum velocity was selected to be 5 mph, as per Specification 2. Subsequently, the thrust force was determined utilizing Equation S1.
\(F = C_d \frac{\rho V^2}{2}A \ \ \ \ \ \ \ ( S1) \)
Here, \(C_d\) is the drag coefficient, \(\rho \) is the density of water, V is the desired robot inlet velocity, and A is the robot’s cross-sectional area. Substituting the known drag coefficient, the assumed velocity of 5 mph, and the area of the robot, the thrust force was determined to be approximately 180 Newtons. Specifically, the area of the robot was assumed to be the cross-sectional area of the square prism. Additional details regarding the decision of the forward velocity to be 5 mph can be seen in Specification #2. Finally, the thrust force was utilized to make several design choices, such as the inlet / outlet dimensions and motor selection.
- The “Forward Velocity” specification is the speed required to move the robot at steady state through still water. Due to the calculated thrust force and required power to the motor shaft, it was determined that 5 mph is a reasonable forward velocity for the robot. Additionally, research into pre-existing RC motorboats was completed to observe the forward velocity of products on a similar scale to our robot. It was determined that the velocity of RC motorboats was slightly greater than 5 mph; to ensure reasonability and feasibility with regards to the speed that the robot could maintain, 5 mph was selected. Given that the robot will be modeled as a 20 x 20 x 20-cm square prism, it was determined that an intake velocity greater than 5 mph would require unreasonably large intake and outtake diameter values. Upon several iterations of the Centrifugal Pump design, it was discovered that an intake diameter greater than 0.07 m and an outtake diameter greater than 0.05 m would require a large amount of motor power for a limited impeller rotational velocity. On the other hand, slightly smaller intake and outtake diameter values would require less motor power to achieve a reasonable impeller rotational velocity.
Essentially, an intake velocity of 5 mph allowed for the Centrifugal Pump design to have reasonable intake and outtake diameters of 0.055 m and 0.035 m, respectively, to ensure that both the Swim sub-system and the Buoyancy sub-system would fit onto a Water Movement chassis. Upon assuming the intake velocity, the corresponding outtake velocity was computed using Equation S2 [S-1].
\(V_{out} = \sqrt{\frac{F_D + \rho V_{inlet} \frac{\Pi}{4}D_{inlet}^2 }{\rho \frac{\Pi}{4} D_{outlet}^2}} \ \ \ \ \ \ \ (S2) \)
The outtake velocity was determined to be 13.97 m/s (31 mph), which was found to be substantially higher than the desired intake velocity. The outlet velocity was calculated using the above formula, which uses parameters independent of the motor specifications. It is also likely that the calculated outlet velocity is an overshoot of what will actually occur; however, it is ideal that the outtake velocity is higher than the intake velocity, to allow for substantial room for error.
- The “Power Consumption” functional requirement is the power required to rotate the motor shaft in order to achieve the computed impeller rotational velocity of 63.65 rad/s. The power was computed using Equation S3 below [S-1].
\(P_{max} = \frac{T_{max}}{\omega_{max}} \omega^2 + T_{max}\omega \ \ \ \ \ \ \ (S3)\)
Here, \(T_{max}\) is the maximum torque, \(\omega_{max}\) is the maximum radial velocity, and ω is the rotational velocity of the impeller. The ultimate goal was to minimize power consumption while achieving the required torque and impeller rotational velocity to maintain an intake velocity of 5 mph. The power was desired to have an upper bound of 150 watts. This value was based on the choice to design the model to last an hour with a 150Wh battery. Upon using Equation S3, the predicted power for the current pump design was determined to be 137 Watts. This power would need to be sent to the motor to achieve an impeller rotational velocity of 63.65 rad/s. Therefore, iterating on the efficiency of the impeller design, as well as the dimensions of the Centrifugal Pump, would allow for a reasonable amount of power to be sent to the motor.
Buoyancy Specifications
| # | Type | Name | Min, Max, or Target | Lower Bound | Upper Bound | Constrained Values | Units |
| B1 | Specification | Depth | Maximize | 1 | Inf | 1 | m |
| B2 | Specification | Pitch and Roll Angle | Target | -5 ° | 5 ° | +-90 ° | θ |
| B3 | Functional
Requirement |
Reservoir Fluid Capacity | Target | 200 | Inf | N/A | g |
- The “Depth” specification is the target depth that the robot should be able to resurface from. This specification is based on IPX7 testing protocol, which states the constrained value is 1m. In turn requiring part of the enclosure to be greater than 1 m below the water surface. Since this depth is a prerequisite for successful waterproofing under the IPX7 standard, at the very least, our robot should be able to resurface from that depth. Deeper water has a higher pressure, so this directly influences the power of the pump that will be used, as for the pump to expel the water when ascending the pump must exceed the current reservoir pressure to resurface.
- The “Pitch and Roll Angle” specification refers to the angles the robot makes with the horizontal. While immersed in water, it is important that the robot can maintain control of its pitch and roll. Forcing the user to manually control the orientation of the robot will add a considerable amount of difficulty. Since shifting cargo and other factors can change the center of gravity of the robot, it would be best for the robot to control its orientation automatically. This specification inspired the decision to create four separate reservoirs. This will allow the robot to distribute water to either side to adjust its center of mass. It is acceptable for the robot to not perfectly match a desired angle, so long as the error is relatively small (around 5°) to represent a flat orientation. In addition, the angle of the robot must not exceed 90° from the horizontal, as this will cause issues with expelling water from the reservoirs.
- The “Reservoir Fluid Capacity” functional requirement refers to the volume of each reservoir that must be achieved in order to ascend / descend in freshwater. This affects how much the robot can change its buoyant force. When the reservoirs have no water in them, the buoyant force should exceed the force due to gravity and when the reservoirs are full – which will not be completely full but rather as much as the pumps can oppose the compressed air within the reservoir – the magnitude of the buoyant force should be smaller than the force due to gravity. Archimedes’ principle states that the desired buoyant force need only be equal to the weight of the robot that exceeds the weight of the volume of water it displaces to be neutrally buoyant. If 200g of water can be displaced by each reservoir our robot should be able to ascend and descend in the water. This was based on the assumption that when integrating with the swim team the robot weight should not exceed 10kg. Allowing for the buoyant force to be roughly 2N in each reservoir and the max pressure to be roughly 50psi, denoting that the ascension and descension can be achieved if the weight is under 10kg.
Legs Specifications
| # | Type | Name | Min, Max, or Target | Lower Bound | Upper Bound | Constrained Value (if applicable) | Units |
| L1 | Functional Requirement | Cost | Minimize | 0 | 1000 | N/A | USD |
| L2 | Functional Requirement | Fold Time | Minimize | 0 | 6 | 10 | sec |
| L3 | Specification | Carrying Capacity | Maximize | 5 | ∞ | 2 | lbs |
| L4 | Functional Requirement | Bending Range | Maximize | 150 (knee)
100 (hip) |
∞ | 100 (knee)
80 (hip) |
deg |
| L5 | Functional Requirement | Tolerance of Angle Measurement | Minimize | 0 | 0.1 | 1 | deg |
- The cost of the legs must be balanced within the total cost of the robot. There is a fairly nebulous upper bound on the budget, somewhere in the low thousands of dollars range. Putting an upper bound of $1000 guarantees that legs will not go over budget and limit the rest of the project. While this upper bound is something to keep in mind while choosing components for manufacturing and the control system, it does not overly limit choices of gears, sensors, etc..
- “Fold Time” refers to the time it would take for the leg to go from fully extended to fully folded or vice versa. The overall objective when designing this aspect of this leg is to minimize this required time in order to satisfy the user’s time management. It would certainly be acceptable for the extension time to be instant or close to zero seconds, but realistically it should remain under six seconds, which is the initial upper bound on what the motor is expected to accomplish. That being said, it would go against optimizing user needs if the extension lasted longer than 10 seconds, because then the infrastructure of the legs could never be applied to something like walking. Other walking robots, like Boston Dynamics’ Spot, take short, quick steps (like in this video on Boston Dynamics’ YouTube channel); it is unreasonable for HARRT’s robot to claim that infrastructure if it cannot move in that timeframe.
- “Carrying Capacity,” in the context of the legs subsystem, refers to the maximum amount of weight the legs can support in operation. The legs will have to support the weight of the chassis, as well as all of the hardware mounted to it. Preliminary estimates place the combined weight of those components at around 5 lbs, providing a basis for a natural lower bound. There is no logical reason to limit the robot’s carrying capacity below some upper bound, as any increase in this respect simply improves its functioning. The constrained value is 2 lbs, the approximate weight of an individual leg. The goal is to maximize the amount of weight the legs can lift so that the robot can fulfill its role as a rescue/support robot.
- “Bending Range” is the maximum angle change through which the knee joint will be capable of moving. This impacts the possible operating configurations of the robot, determining the difference between the “fully extended” and “fully folded” positions. While in operation, the lower the robot’s center of gravity, the larger the force or perturbation will be required to cause tipping, making it more dynamically stable. Thus, it is desirable for the robot to have the ability to lower its center of gravity as much as possible. In order to help satisfy this specification, the leg sections were designed to be concentric channels so that only the eventual interference with the wheels or treads themselves would limit the complete folding of the legs. This geometry of the joints does not allow a full 360 degree range of motion. To fully fold and fully extend the legs, it is reasonable to expect that the hip will need at least 80 degrees and the knee will require at least 100 degrees of rotation. Optimally, both joints will have greater ranges of motion, at or above the lower bound of 100 and 150 degrees respectively.
- Angle measurement of the legs is being able to tell at any time where the legs are, which is necessary to implement closed-loop control. The sensors are angle position potentiometers placed on one of the shafts at each joint; the more accurate these are, the better the control system will be. Each leg needs to be consistent with the other legs so that the robot does not tilt or pull the tracks apart. Analysis revealed that no error in angle sensing could cause the robot to fall either along its long or short axis. Accuracy to one-tenth of a degree will maintain less than 25 thousandths of an inch of pull/push on the tracks, which is reasonable to expect will not break them. If the leg cannot achieve a 1% tolerance, which will correlate to approximately 1 degree with the expected range of motion, then it is unrealistic to base a controller on that measurement without damage to the motor/transmission. With the width of the robot as currently imagined, there is no inconsistency between the legs that would cause it to lose its balance. The sensors chosen have essentially infinite resolution, so they should be perfect for the system.
Treads/Wheels Specifications
| # | Type | Name | Relevant Subsystem/Function | Min, Max, or Target | Lower Bound | Upper Bound | Constrained Value (if applicable) | Units |
| TW1 | Specification | Ground Speed | Leg-Wheel Interface | Maximize | 1 | ∞ | N/A | m/s |
| TW2 | Specification | Angle of Traversable Slope | Tracks | Maximize | 40 | 90 | N/A | deg |
| TW3 | Specification | Ground Clearance | Suspension | Target | 30 | 120 | 15 | mm |
| TW4 | Functional Requirement | Motor | Leg-Track Interface | Target | 2.5 | 5 | N/A | N•m |
| TW5 | Specification | Suspension Weight Capacity | Suspension | Target | 20 | 60 | N/A | kg |
- The “Ground Speed” specification is the speed at which the robot can travel on different terrains. This specification should be maximized as to best assist in a disaster relief situation. The 1 m/s is the unloaded minimum speed on level terrain. The minimum speed that would be sufficient would be 1 m/s as it will be able to travel across various terrains effectively. This lower bound is selected based on the average walking speed of a human which is 1.2-1.4 m/s (Chui et al. 2019), if the robot is significantly slower than the human walking pace it will be inefficient in providing relief in disaster scenarios. The ground speed will change in relation to the additional weight on the robot as the acceleration of the robot will change. The ability to reach higher ground speeds will allow for the robot to better address rugged terrain and hills. This is imperative so that the robot can be dispatched without the need for human interference. [TW-1]
- The “Angle of Traversable Slope” specification is the maximum angle on a specified terrain that the robot should be capable of traversing. For the given goals of the land movement subteam, a functional prototype consisting of a chassis, four legs, and two sets of treads should be able to scale a flat, 40-degree slope. This value for the specification was chosen based on being a commonly achievable goal for tracked vehicles of similar size and weight (Endo). The ability to perform this specification is dependent on several factors: tread design, torque of motors, weight distribution of the robot, and the robot’s ability to maintain traction/prevent slip. While the tread design of the tracks has not been finalized, multiple versions will be tested to gauge which is the best performing. Tread design contributes significantly to the robot’s ability to maintain traction. However, the surface of the test terrain is also highly impactful. For this reason, the test slope should be covered in some rough or coarse material to facilitate traction. This could be accomplished by roughing up the surface of the test slope or covering it in a material such as grip tape. Initial calculations were performed prior to the design of driving components to choose an appropriate motor for operating conditions. With the preliminary design notes, it was decided that the chosen motor would be suitable with a change in gear ratio to meet the angle of attack specification. The final aspect that contributes to the robot’s ability to meet this criterion is that of weight distribution. This factor is dependent on the ability of the legs sub-team to place the chassis in an optimal position, given the relatively high center of mass, even while the robot is in a squatted position. To best fulfill this specification, the chassis should be positioned with a forward bias to prevent it from tipping backward while scaling the slope. The impact of this specification is in the robot’s ability to scale obstacles and sloped terrain. [TW-2]
- The “Ground Clearance” specification is the total distance between the bottom of the tracks and the next lowest interfering surface of the robot, being the compressed suspension-spar subsystem of the tracks (shown as \(G_{cl}\) in the figure below). This specification is also heavily linked to the compression distance of the suspension. From a functional standpoint, the ground clearance effectively dictates the maximum height of an obstacle the robot can encounter without significant change in its pitch. Furthermore, increasing the ground clearance helps prevent the robot from being stuck on an obstacle without having sufficient track/wheel traction to move the system. That being said, excessive ground clearance may lead to an unnecessary increase in height of the vehicle’s center of gravity, making it more susceptible to tipping. As such, a balance of clearance distance is required. For our robot, the constrained value of 15 mm of clearance accommodates for small sticks, gravel, and debris. Ideally, we would have 30 mm, which could handle small step changes in the ground, larger pebbles, and more. Exceeding 120 mm would allow for larger rocks, bottles, and other obstructions; however, given the size of our robot, this would likely detract from its overall stability. To achieve these values, we are utilizing MATLAB simulations to determine the necessary suspension compression length and orientation required to be designed around in CAD.
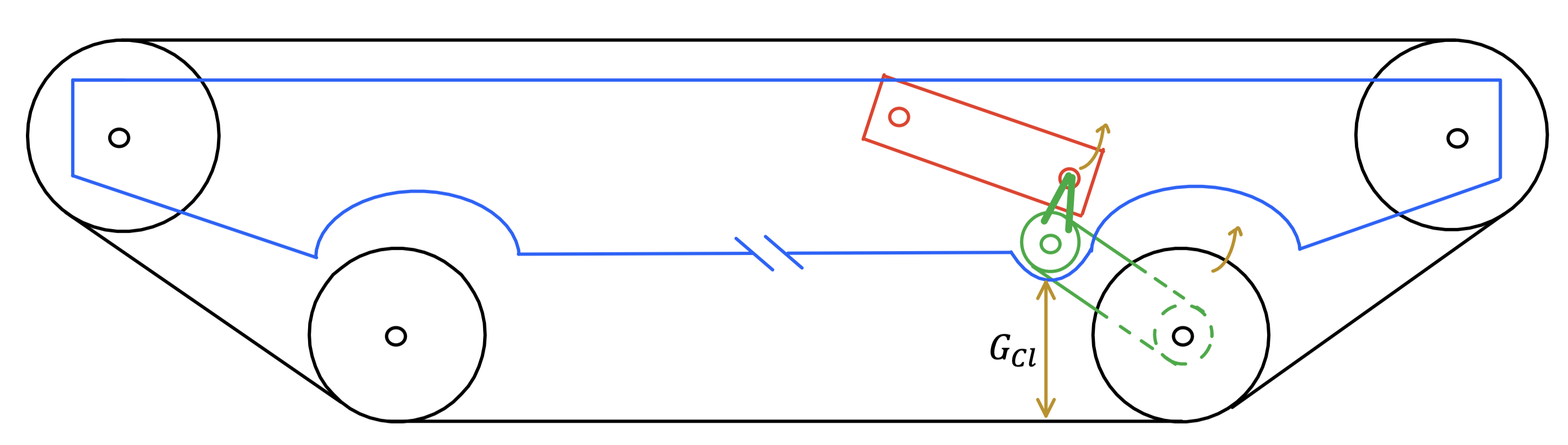
- The motor choice functional requirement is closely linked to all three of the previous specifications. In being able to deliver the power necessary to meet the ground speed requirements, a motor of sufficient torque and rpm values is needed. Assuming that the final product exists with little internal resistance, all that would be necessary to propel the robot at the specified rate is a proper available motor RPM and correct gearing. Unlike the ground speed specification, the angle of attack specification relies more heavily on the available torque of the motor. In both being able to maintain a static state on an inclined (or declined surface), the motor must be able to resist the force of gravity pulling the robot down said slope. Even more strenuous on the motor is the necessity to be able to propel itself up the aforementioned incline. For this, a force analysis was done to give an approximate torque rating for the robot to be able to scale a slope of around 40 degrees. This analysis returned a value of 2.5 N•m per motor. Given that there are two motors per track, this would provide 5 N•m of available torque, which should be sufficient to allow the robot to scale the specified slope. While exact measurements are unknown for small objects of varying shapes, increased torque would benefit the suspension system in being able to scale these obstacles.
- The “Suspension Weight Capacity” specification is the maximum load the suspension can support before reaching maximum compression. Ideally, the suspension should at least be able to support the weight of the chassis/overall robot without significant compression. If the chassis’s weight significantly compresses the suspension, the effectiveness of the suspension is significantly reduced in providing a smooth and level ride. The lower bound of this specification is based on supporting a Level 2 chassis such that only the Legs and Treads/Wheels systems are being supported. Although original intentions were for the robot to be able to support up to 40 kg, the upper bound is capped at 60 kg. Supporting increasingly heavy loads requires stiffer suspension. If the suspension is made too stiff in order to support an unrealistic maximum load, the suspension’s effectiveness at lower loads will be significantly reduced as the system will become more rigid with reducing weight.
Citations:
S-1. Gerhart, Philip M., Andrew L. Gerhart, John I. Hochstein, Bruce Roy Munson, Donald F. Young, and T. H. Okiishi. Munson, Young, and Okiishi’s Fundamentals of Fluid Mechanics. Wiley, 2016.
TW-1. Chui, K. C., Jorge, M., Yen, S. C., & Lusardi, M. M. (2019). Orthotics and Prosthetics in Rehabilitation E-Book. Elsevier Health Sciences.
TW-2 Endo, D., Nagatani, K. Assessment of a tracked vehicle’s ability to traverse stairs. Robomech J 3, 20 (2016). https://doi.org/10.1186/s40648-016-0058-y
