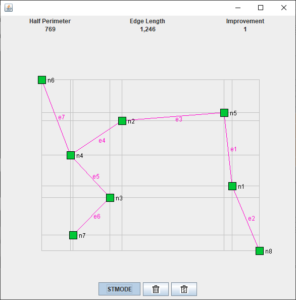
This app illustrates how a Steiner Rectilinear Tree (SRT) can be constructed by adding Steiner Points to an existing set of terminals. The user can edit the number and location of a set of terminals and then add and/or delete Steiner points to evaluate their effect on the length of the resulting tree. The app then displays the Rectilinear Minimum Spanning that includes both the terminals and Steiner points to form a Steiner Rectilinear Tree.
A Minimal Steiner Rectilinear Tree (MSRT) is a minimum-length Steiner Tree. This app does not compute the minimal Steiner Tree but instead lets the user experiment with different choices of Steiner points to discover their impact on overall length.
To Use the App
Terminals are displayed as small squares; Steiner points are displayed as circles. Edges show the edges of a Rectilinear Minimum Spanning Tree that connects terminals and Steiner Points.
The app operates in two modes: Terminal Edit mode, and Steiner Point Edit mode. The user can switch between the two modes by clicking the “STMODE” button.
Terminal Edit mode is used to add, delete, or move terminal nodes as follows:
- Add a terminal by clicking at a location where no terminal exists.
- Move a terminal by clicking and dragging it to the desired location.
- Delete a terminal by pressing the CONTROL key and clicking.
While in Terminal Edit mode the app computes and displays the rectilinear Minimum Spanning Tree (RSMT) of the terminal points after each change.
In Steiner Point Edit mode, Steiner points may be added and removed at locations on the “Hanan Grid”, which is shown in gray (see explanation below) as follows:
- Add a Steiner point by clicking at a location on the Hanan Grid.
- Remove a Steiner point by pressing the CONTROL key and clicking.
While in Steiner Pont Edit mode, the Steiner tree that results from the selected points is computed using the RMST algorithm and displayed along with the improvement in cost over the RMST without added Steiner points.
If you’re interested, here is the source code
About Steiner Trees
Given a set of terminal points in a plane, a Minimum Steiner Rectilinear Tree (SRT) is a set of edges that connects all the terminals along with a set of added “Steiner points” such that the rectilinear distance is minimized. F. Hwang [Hwang, 1976] proved that the length of a Steiner tree can be up to 3/2 times shorter than a Rectilinear Minimum Spanning Tree on the same set of terminals.
M. Hanan [Hanan, 1966] proved that a Minimum RST can be constructed using points on a grid defined by the x and y coordinates of the terminal points (now known as the Hanan Grid).
The Minimum Steiner Rectilinear tree problem is NP-Hard [Garey, 1977], which indicates that any exact algorithm will have a worst-case execution time that grows exponentially with the problem size. In spite of this, exact algorithms such as have been found that complete in a reasonable time for large examples [Warme 2003].
Several heuristics have also been developed; we plan to add a brief survey along with animations of some key heuristics in the future.
References
J. Ganley, P. Madden, G. Robins, and I. Mandoiu, “GSRC Bookshelf Rectilinear Steiner Minimum Tree Slot”, February 2003. http://vlsicad.ucsd.edu/GSRC/bookshelf/Slots/RSMT/.
J. Ganley. “The Steiner Tree Page”, http://ganley.org/steiner.
M. Sarrafzadeh and C. K. Wong, An Introduction to VLSI Design, McGraw-Hill, 1996.
M. Garey and D. Johnson, “The rectilinear Steiner tree problem is NP-complete”, SIAM Journal on Applied Mathematics, Vol. 32 pp. 826-834, 1977.
M. Hanan, “On Steiner’s Problem with Rectilinear Distance”, SIAM Journal of Applied Math, Vol. 14, No. 2, March 1966, pp. 255-265.
F. Hwang, “On Steiner Minimal Trees with Rectilinear Distance”, SIAM Journal of Applied Mathematics, Vol. 30, No. 1, January 1976, pp. 104-114.
F. Hwang, D. Richards, and P. Winter, The Steiner Tree Problem, North-Holland, 1992.
D. Warme, P. Winter, and M. Zachariasen, “GeoSteiner 3.1 Home Page”, January 2003 http://www.diku.dk/geosteiner.
Acknowledgment
This RMST code used in this app is derived from Joseph Ganley’s “Interconnection Tree Applet”, which can be found at http://ganley.org/software/tree.html