This app illustrates the construction of a Rectilinear Minimum Spanning Tree (RSMT) using Prim’s Algorithm. An RMST connects all terminals together in a way that minimizes the overall distance of the connections in this tree. Prim’s Algorithm operates incrementally on a partial tree starting with a single terminal – on each iteration, it adds an edge between the partial tree and the terminal that is closest to any terminal in the partial tree.
To Use the App
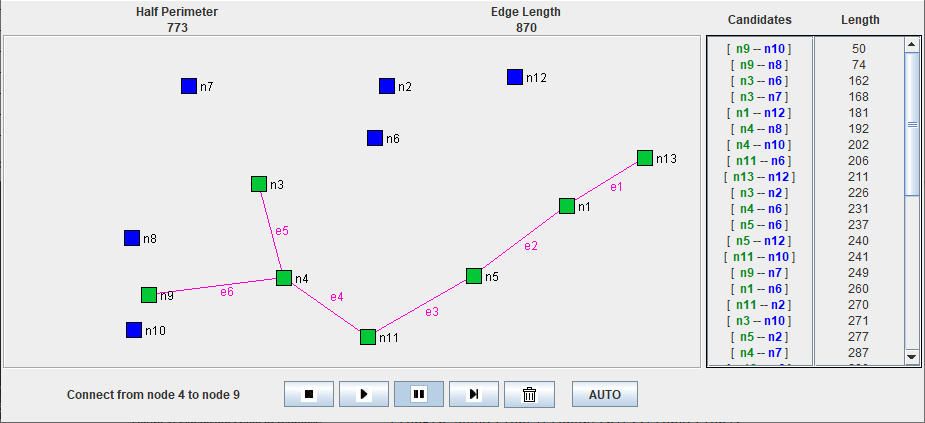
This app creates a small number of terminals at random locations. Use the “VCR” controls to start, pause, single-step, or stop the animation.
There are several ways to edit the terminals shown in the animation:
- Add a terminal by clicking at a location where no terminal exists.
- Move a terminal by clicking and dragging it to the desired location.
- Delete a terminal by pressing the CONTROL key and clicking over an existing terminal.
Note that editing terminals will stop a running animation since the previously executed steps may no longer be valid.
Clicking the “AUTO” button places the app in automatic mode, where the complete RMST is recalculated
whenever the terminals are edited or moved.
A distance table is placed in the right area of the window to display the length of each edge candidate in ascending order so that which edge should be connected will be clear.
If you’re interested, here is the source code
About Rectilinear Minimum Spanning Trees
Given a set of terminal points in a plane, a rectilinear minimum spanning tree is a set of edges that connects all the terminals with minimum rectilinear distance. Rectilinear distance (also called “Manhattan Distance”) is the sum of the horizontal and vertical distance between two points. It is used instead of Euclidean distance in VLSI CAD applications because VLSI processes support only horizontal and vertical wires.
The RMST can be used as an estimate of the length of a net that connects multiple terminals.
The RMST Problem is a special case of the Minimum Spanning Tree problem studied in Computer Science Algorithms textbooks in that the distances between the points imply a complete graph.
References
A. Kahng and I. Mandoiu, “GSRC Bookshelf RMST-Pack: Rectilinear Minimum Spanning Tree Algorithms”, June 2001. http://vlsicad.ucsd.edu/GSRC/bookshelf/Slots/RSMT/RMST/.
M. Sarrafzadeh and C. K. Wong, An Introduction to VLSI Design, McGraw-Hill, 1996.
Acknowledgment
This RMST code in this app is derived from Joseph Ganley’s “Interconnection Tree Applet”, which can be found at http://ganley.org/software/tree.html